Medición de longitudes utilizando un teodolito casero

Aprendizaje basado en Situaciones Problémicas

Problema 1: Hallar la distancia entre un punto (A) ubicado en el techo del salón de clases y un punto (B) ubicado en una esquina de la cancha.

Problema abordado desde la trigonometría

Se pretende a través de la construcción de herramientas caseras, dar solución a esta situación problémica cotidiana, aplicando la tiangulación, es decir, cálculos básicos de ángulos y longitudes en triángulos, que son elementos dados por la geometría y la Trigonometría.

Conceptos previos:
Teorema de Pitágoras
Definición de Distancia en el plano.
Razones Trigonométricas
Medidas de Ángulos y su caracterización.

Herramientas de Trabajo:

El Teodolito, cinta métrica, calculadora científica, escuadras, elementos de escritorio(cuaderno de notas, lápiz, borrador).

El Teodolito es una herramienta usada especialmente por los ingenieros Civiles para ubicar un objeto a cierta distancia mediante la medida de ángulos con respecto al horizonte y con respecto a los puntos cardinales.

Fig. 1: El primer teodolito fue construido en 1787 por el óptico y mecánico Jesse Ramsden.

Guía de trabajo

Los estudiantes y personas que quieran dar solución a esta situación problémica a traves de la utilización del teodolito, d eberán construirlo como se muestra el la figura 2 y seguir las demás indicaciones después de esto.

1. Construcción
Hacemos un trípode con trozos de madera de igual longitud y acorde a la estatura de las personas que lo vayan a usar. A partir de éste ponemos un tubo delgado o pitillo de un tamaño suficiente y que pueda moverse libremente para facilitar una "mira" o la referencia hacia el punto objetivo hasta donde queremos medir; le sujetamos a éste un cordel (pita, fibra) que sea resistente y que pueda sujetar una pequeña plomada. Ubicamos estratégicamente un transportador que se mueva paralelamente al pitillo, de tal manera que al mirar el punto objetivo, la plomada nos indique a través del cordel el ángulo de elevación respecto a un plano paralelo al piso. Ver figura 2.

Fig. 2: Un teodolito costruido de forma casera

2. Indicaciones

Como se explicó en la construcción del Teodolito Casero, éste se utilizará para medir dos ángulos de elevación respecto a un plano paralelo al piso, a saber: los ángulos alpha y Beta. Ver figura 3. Primero se halla el ángulo alpha desde un punto B que es nuestro punto de referencia, luego se recorre una distancia a, luego se vuelve a medir otro ángulo, a saber el Beta y se registran estos datos en un cuaderno, para luego hacer los respectivos cálculos que nos conducirán a hallar la distancia entre los puntos A y B.

Figura 3: Planteamiento Geométrico para la solución del problema 1.

3. Cálculos básicos para hallar la distancia entre los puntos A y B.

Mediante los siguientes cálculos se dará una propuesta de solución al problema 1, tomando como ayuda visual la figura 4:

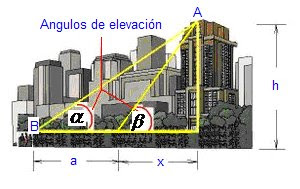
Figura 4: Triangulación en donde se plantean tres incógnitas

A saber, los ángulos Alpha y Beta Son conocidos y la longitud “a” es conocida.

Las longitudes “x”, “d” y “h” son desconocidas. Se debe encontrar “d”.

Aplicando las relaciones trigonométricas se sabe que:

4. Estimación de la distancia real:

Como en las mediciones de los ángulos se pueden tener errores, debidos al paralaje, a una mala visión, y en general a la intervención humana que puede ser subjetiva, es importante entonces tomar las mediciones varias veces y hallar una estimación estadística y el error relativo.

En la siguiente tabla se consignarán los datos de las mediciones que se tomarán en la práctica con el teodolito que construyeron y se realizarán algunos cálculos:

Tabla 1: Datos de la práctica con el teodolito

Ángulo	M1	M 2	M3	M4	M5	Promedio	Desviación Estándar	Error Relativo
Alpha
Beta

Si la distancia d, real es: _____________

Entonces calcular el error relativo de la distancia que hallaron y los ángulos que encontraron en la práctica con el Teodolito.